Introduction

Radiation is an important energy transfer mechanism in thermal plasmas that exists during high current interruption in electrical switching devices, such as circuit breakers or contactors. In these applications an electric arc exists between the electrical contacts and radiation is emitted from the arc core, contributing to the cooling of the arc. Radiation absorbed by walls lead to evaporation of wall materials and influences the properties of the plasma. It is therefore important to properly evaluate the radiative energy transport while modeling the arc in switching devices in order to support their design process.

Several approximate methods to calculate the radiation transfer inside plasmas have been developed, like the simplified Net Emission Coefficient (NEC) model [1], the P1 model [2] or the more sophisticated and precise Discrete Ordinates Method (DOM) [2]. These methods are simplifying the spatial description of the radiation transfer. To evaluate the total energy transfer, the entire spectrum has to be considered (integrated) in all these methods which makes the radiation transfer calculation a very demanding task regarding the necessary compute power. The reason is that the absorption coefficient spectrum is usually very complex, containing both continuum contribution and a narrow spectral lines whereas the spectral intensity can vary several orders of magnitude in the spectral range that is usually considered [3]. To achieve a reasonable resolution of the spectrum, it is often required to use several hundred thousands of frequency steps when using line-by-line methods [4]. But even if lines are treated separately from the continuum (for example by method of escape factors described in [5]), the number of lines is usually in the order of several thousands. This number is still too high requiring considerable computation time or large lookup tables.

The computational effort associated with spectral radiation transfer calculations makes this approach unsuitable for applications with complex geometries. To evaluate the radiation with at least some level of accuracy, the method of mean absorption coefficients (MAC) is usually used [6], even though it is not the only one [7]. Hereby the entire spectrum is divided into several frequency intervals (bands) and in each band the absorption coefficient is considered to be constant. This approach effectively reduces the computation time needed to solve the radiation transfer calculation, because the radiation transport equation needs to be solved only for a small number of bands rather than for a huge number of small steps (line-by-line method) to resolve the entire spectrum. The drawback of using MACs in simulations is the reduction of accuracy of the radiation transfer calculation.

There are several questions related to the application of mean absorption coefficients, e.g. which approach can be used to calculate the mean absorption coefficient for each band. General options therefore are either Planck or Rosseland averaging [2]. In case of Planck averaging some form of line limiting procedure is usually applied in order to increase the accuracy [6].

A further question is how the integration intervals (bands) can be properly selected in order to get a reasonable level of accuracy in the radiation transport model. Therefore the number of bands as well as the location of the integration boundaries need to be determined. Because the computational effort can be high even if only a couple of bands are used, the number of bands that should be used is really a question of the required accuracy versus the computational effort one is willing to devote to the radiation calculation. Additionally the selection of the integration boundaries (and therefore also the width of each band) has an important influence on the accuracy. Yet there is no clear guideline available how to define these intervals. Peyrou [8] only gives the advice that the absorption coefficient should not vary strongly within one band. Nordborg and Iordanidis [6] used the variation of the spectral absorption coefficient with temperature as the base for the band selection. Hannachi et al. [13] grouped the absorption coefficient into bands based on the energies and important processes in the considered mixture, while Jan et al. [14] based their band distribution on the variation of the absorption continuum. Reichert et al. [9] successfully used 7-band MAC radiation model in commercial CFD program but unfortunately did not state the method they used for the band selection. It is thus clear that the proper band selection is a very complex task.

In this work we show that the selection of the integration intervals is indeed not obvious. We demonstrate that the simple approach using the frequencies where the continuum absorption coefficient shows a step-like change as integration boundaries can produce inaccurate results in some cases. Since there is no evident definition where the band boundaries should be located in order to get the best accuracy, there is a need for an systematic approach to determine these. As it is shown in this paper, many variables such as absorption coefficient profile, mean approximation, temperature profile and even optical thickness influence the optimal band distribution. Numerical optimization seems to be the only way how to properly handle these parameters in a systematic way. We propose the objective function for the optimization process and suggest what properties this optimization process needs to handle.

The main part of this paper is divided into three sections. The first one describes the radiation transfer model which is used to evaluate the accuracy of the MAC based approach. In the second part the influence of the selection of different integration boundaries is demonstrated by means of several simplified test cases. In the last part we show how difficult the boundary selection problem gets when an absorption coefficient spectrum of a gas is taken into account.

Model

The evaluation of the MAC accuracy can be divided into three subsequent steps. In the first step the spectral radiation transfer is calculated, resolving the whole spectrum. In the second step the radiation transfer within the same domain is calculated substituting the spectral absorption coefficient by two-band MAC based model. Finally the difference between results from steps one and two are evaluated.

First Step

The model used to calculate the spectral radiation transfer (referenced as exact in this paper) can be characterized as a one dimensional DOM model and was more thoroughly described in [10]. The calculation domain has a shape of an infinite plasma cylinder with 1 cm radius and an axisymmetrical temperature profile. To test the influence of the temperature profile, several distinct profiles were used. They are schematically depicted in Fig. 1 including a single constant temperature profiles. The non-constant profiles are designed to have a temperature maximum of 25 kK in the center, which is a reasonable value for an arc in circuit breakers [11]. As there is no direct connection between our defined test cases and real plasma configurations, there is no restriction on the selection of the outer boundary temperature. The temperature profiles are designed to have an outer temperature of 5 kK, which allows for a faster calculation of the blackbody fraction belonging to the first band (compared to lower temperature) in the next step. The temperature for constant temperature profiles is also chosen within this temperature range, plus an additional profile with 30 kK temperature value.

Fig. 1
figure 1

Temperature profiles considered in the calculations

Full size image

The absorption coefficient spectrum used in this step is referred to as exact absorption coefficient in the text and is considered to be independent of temperature. A fine spectral resolution with a frequency step size of \(10^{11}\) Hz is chosen (from approx. 3 nm to approx 0.0012 nm depending on wavelength in the considered spectral range). The exact absorption coefficients defined in the section “Test Cases” part do not reflect any real physical absorption coefficient, they are rather chosen arbitrary to demonstrate the influence of the integration procedure on the MAC model results. In the section “More Realistic Spectrum” the exact absorption coefficient reflects the absorption coefficient of air at a temperature of 20 kK and pressure of 1 bar.

In order to compare the spectrally resolved model results with the MAC model results, the divergence of the radiation flux \(\nabla {\cdot } {\mathbf {F}}_{\text{ex}}\) inside the domain is calculated at 20 spatial points evenly distributed along the cylinder radius. The number of spatial points was chosen as a reasonable compromise between the computational time and accuracy also considering that \(\nabla \cdot {\mathbf {F}}_{\text{ex}}\) varies slowly along the radius for the considered test cases. The exact calculation method is described in [10]. This provides enough points for comparison in the third step while still keeping the computation time reasonably low.

Second Step

The same numerical model as in the first step is used in the second step, but here the exact absorption coefficient is substituted with a two-band MAC. For the sake of clarity, only Planck mean averaging approach was used to calculate the MAC inside each band. Even though the exact absorption coefficient was considered independent of the temperature, the resulting MAC are temperature dependent. This is due to the definition of the Planck mean averaging

$$k_m = \frac{1}{\int _{\nu _1}^{\nu _2} B_{\nu }(T) {\text {d}}\nu }\int _{\nu _1}^{\nu _2} k_{\nu } B_{\nu }(T) {\text {d}}\nu,$$
(1)

where \(k_m\) denotes the mean absorption coefficient in a band limited by frequencies \(\nu _1\) and \(\nu _2\), \(k_\nu \) is the exact (spectral) absorption coefficient and \(B_\nu (T)\) is the Planck function. Since the Planck function is temperature dependent, the resulting mean absorption coefficient depends on temperature too. The relation (1) is not adapted for the presence of the strong lines as there are no strong lines considered in the test cases.

The frequency which defines the boundary between the two frequency bands is referred to as break point \(p_\nu \) in the text. In order to analyze the influence of the integration interval, we varied the break point location \(p_\nu \) from the lower to the upper frequency limit and calculate each time the divergence of radiative flux \(\nabla {\cdot } {\mathbf {F}}_{{\text{MAC}}_\nu}\) for each of the 20 points. All these data sets are then used in the third step to evaluate the accuracy.

Third Step

The difference between the results of the first step and the second step are evaluated here. We do the evaluation by calculating a norm defined as

$${\varDelta} {F_{\nu}} = \frac{1}{20}\sqrt{\sum _{i=1}^{20}{\alpha _i}\left( \nabla {\cdot } {\mathbf {F}}_{{\text{ex, i}}} - \nabla {\cdot } {\mathbf {F}}_{{\text{MAC}}_\nu, i} \right) ^2},$$
(2)

where \(\alpha _i\) is a weight of each point i. In this paper the weight is considered constant \(\alpha _i = 1\). Note that it is possible to set \(\alpha _i = \left( \nabla \cdot {\mathbf {F}}_{{\text{ex,i}}} \right) ^{-2}\) in which case the norm would have meaning of a relative error. This definition would emphasize an areas with low values of divergence of radiation flux (i.e areas where \(\nabla \cdot {\mathbf {F}}_{{\text{ex,i}}}\) tends to zero) and therefore would produce significantly different results. With our choice of \(\alpha _i = 1\) we do not emphasize any area.

The norm provides a good description of the difference between the results using the exact (spectral) absorption coefficient and the mean absorption coefficient (MAC). It also allows to plot the norm \({\varDelta} {F_{\nu}}\) as a function of the break point location \(p_\nu \) (frequency) and to determine the location with best agreement and therefore best accuracy (minimum of norm \({\varDelta} {F_{\nu}}\)).

It is often useful to express the norm as a relative value rather than the absolute value. For that purpose we define reduced norm

$${\varDelta} {F_{\nu}^{\prime}} = {\varDelta} {F_{\nu}} \left( \frac{1}{20}\sum _{i=1}^{20} \nabla \cdot {\mathbf {F}}_{{\text{ex,i}}} \right) ^{-1}.$$
(3)

However we do not plot this reduced norm in the figures in the following test cases. The reason is the readability of those figures. The reduced norm is usually the same within one test case and would produce hard to read overlapping lines. Therefore we just mention the value of the reduced norm in the text.

Test Cases

In this section we demonstrate by means of several test cases that the optimal position of the integration boundary cannot always be determined just by looking at the variances in the exact absorption coefficient. For each case we first introduce the exact absorption coefficient and describe what effect we are going to simulate. Then we plot the corresponding norm \({\varDelta} {F_{\nu}}\) of the two band approximation as the function of break point \(p_\nu \). We determine the position of the minimum of the norm which is the best match between the spectral and the MAC model and derive some conclusions. We also mention the range of reduced norm \({\varDelta} {F_{\nu}^{\prime}}\) so that it is easier to understand the relevance of the results.

Test 1

The first test is designed to show the general behavior of the two-band MAC model. The exact (spectral) absorption coefficient we define here has a profile which is similar to the two-band MAC profile, as shown in Fig. 2. The range of the absorption coefficient was defined between 1 and 10 m\(^{-1}\). The reasons for using this particular value and range are following. We tried to avoid a situation where the medium can be considered extremely optically thin or thick. With the absorption coefficients varying from 1 to 10 m\(^{-1}\), the optical thickness (calculated as integral of the absorption coefficient along the radius of 1 cm) varies from 0.01 to 0.1. According to [12] this values are in optically thin region yet very close to the transition area. The optically thin limit is postulated to be 0.25. Additionally the selected values are close to a values for realistic MACs at atmospheric pressure [13]. The relatively small range (compared to variation of a real spectral absorption coefficient) is selected to make any shifts in the minimum of the norm \({\varDelta} {F_{\nu}}\) more visible. This effect is discussed more thoroughly in the Test 3.

In this test case the evaluation of Eq. (2) is expected to result in a zero value at the frequency of the step-like change in the exact absorption coefficient (break point) and deviate from zero elsewhere. However, the actual results deviate from the expectation as shown in Fig. 2, where a non-zero value for the norm is achieved at the break point. There are several factors contributing to this discrepancy. The first one is the exact numerical positioning of the break point \(p_\nu \) in the calculation. If there is just a slight deviation from the frequency of the step-like change in the exact absorption coefficient, a rapid increase of the norm \({\varDelta} {F_{\nu}}\) can be observed. We tried to minimize this effect in this test case by calculating one additional point at the exact frequency of the MAC jump. However, this additional point was omitted in the other test cases as it was not necessary to know the exact position of the minimum \({\varDelta} {F_{\nu}}\), we are more interested in the general behavior of the norm \({\varDelta} {F_{\nu}}\).

The second factor causing the norm \({\varDelta} {F_{\nu}}\) to deviate from zero is the difference in the numerical integration of the radiation term, namely

$$\varepsilon = \int _{\nu _1}^{\nu _2} k_{\nu }\,B_\nu \,{\text {d}}\nu.$$
(4)

In the first step the direct integration is done using a trapezoidal integration scheme. In the second step, the absorption coefficient \(k_\nu \) is considered constant within one band and refactored as a constant out of the integration procedure. The remaining integral is then calculated using fractions of the blackbody emissive power, as described by Modest [2]. The results will slightly differ and thus the norm is not calculated as an exact zero value.

The last factor contributing to the difference is a rounding error of double precision variables used in the calculation. Even though this introduces relatively marginal error it still can prevent the norm \({\varDelta} {F_{\nu}}\) to become an exact value of zero.

The absolute value of the norm is therefore less important than its general behaviour. The norm minimum is always located at the frequency of the step-like change in the exact absorption coefficient independently of the plasma temperature or temperature profile used during the evaluation as shown in Fig. 2. The relative values given by the reduced norm are within the range from 0.008 to 0.014 at the maxim values and going down to \(10^{-6}\) at the minimum. The notable exception is the 5 kK constant temperature profile with the maximum value of \(2\times 10^{-6}\).

Fig. 2
figure 2

The difference between exact and two band model as the function of the break point location (frequency integration boundary) for constant temperature profile (a) and varying temperature profiles (b). This figure illustrates results from test 1

Full size image

Test 2

In the second test case the exact (spectral) absorption coefficient is defined to represent two equal step-like changes. The profile can therefore be described as a trench, where the depth of this trench like profile is chosen relatively large so that the influence on the MAC is significant. As in the previous test, the MAC is defined by two bands where the joint frequency integration boundary location is varied (break point).

The obtained dependence of the norm \({\varDelta} {F_{\nu}}\) on the location of the break point \(p_\nu \) for different temperature profiles is shown in Fig. 3. For all the temperature profiles, two minima were obtained corresponding to the location of the jumps in the exact (spectral) absorption coefficient. The norm values at these locations do not reach the same level, therefore one of the two frequencies can be considered as the global minimum and the other frequency is a local minimum only. The maximum values of the reduced norm are in range of 0.01 to 0.006 and the minimum values for each profile are approximately 0.004 lower. Yet again this does not apply to the constant temperature profile at 5 kK where the reduced norm is significantly lower at around \(3\times 10^{-4}\).

Fig. 3
figure 3

The difference between exact (spectral) and two band model as the function of the break point location (frequency integration boundary) for constant temperature profiles (a) and varying temperature profiles (b). This figure illustrates results from test 2

Full size image

In the case of an isothermal plasma, it is possible to determine which of the two possible frequencies will represent the global minimum. The determination is based on assumption that the divergence of the radiative flux inside isothermal, non-scattering, and participating medium surrounded by non-reflexive walls can be expressed by the simple equation

$$\nabla {\cdot } {\mathbf {F}}({\mathbf {r}}) = \int k_{\nu }\, B_{\nu }(T)\, F(k_{\nu }L, {\mathbf {r}})\, {\text {d}}\nu,$$
(5)

where \(F(k_{\nu }L, {\mathbf {r}})\) is a geometric function describing the calculation domain, L is some characteristic length and \({\mathbf {r}}\) is the relative position of a point in which the divergence of the radiative flux is being calculated. In our test case, the exact (spectral) absorption coefficient is represented by a step-like function. Lets assume that the break point \(p_\nu \) is positioned at the frequency of one of the step-like changes. In this case one mean absorption coefficient band out of our two-band approximation exactly corresponds to the exact (spectral) absorption coefficient and does not contribute to the norm \({\varDelta} {F_{\nu}}\). Therefore the band that contributes to the norm \({\varDelta} {F_{\nu}}\) is only the one that contains the second step-like change.

If we denote the frequency of the step-like changes in the exact (spectral) absorption coefficient as \(\nu _{{\text{c}}1}\) and \(\nu _{{\text{c}}2}\) respectively (\(\nu _{{\text{c}}1} < \nu _{{\text{c}}2}\)), the aforementioned band ranges either from 0 to \({\nu _{{\text{c}}2}}\) or from \({\nu _{{\text{c}}1}}\) to infinity respectively. Using (5) the contribution from one spatial point \({\mathbf {r}}\) to norm \({\varDelta} {F_{\nu}}\) can be calculated as either

$$\begin{aligned} \varDelta F({\mathbf {r}})=\,&\left[ k_1 F(k_1 L,{\mathbf {r}}) - k_{{\text{MAC}}_\nu } F(k_{{\text{MAC}}_\nu }L, {\mathbf {r}})\right] \int \limits _0^{\nu _{{\text{c}}1}} B_\nu (T) {\text {d}}\nu \\&+ \left[ k_2 F(k_2 L,{\mathbf {r}}) - k_{{\text{MAC}}_\nu } F(k_{{\text{MAC}}_\nu }L, {\mathbf {r}})\right] \int \limits _{\nu _{{\text{c}}1}}^{\nu _{{\text{c}}2}} B_\nu (T) {\text {d}}\nu \end{aligned}$$
(6)

or

$$\begin{aligned} \varDelta F({\mathbf {r}})=\,&\left[ k_2 F(k_2 L,{\mathbf {r}}) - k_{{\text{MAC}}_\nu } F(k_{{\text{MAC}}_\nu }L, {\mathbf {r}})\right] \int \limits _{\nu _{{\text{c}}1}}^{\nu _{{\text{c}}2}} B_\nu (T) {\text {d}}\nu \\&+ \left[ k_3 F(k_3 L,{\mathbf {r}}) - k_{{\text{MAC}}_\nu } F(k_{{\text{MAC}}_\nu }L, {\mathbf {r}})\right] \int \limits _{\nu _{{\text{c}}2}}^{\infty } B_\nu (T) {\text {d}}\nu \end{aligned}$$
(7)

respectively. The variables \(k_1\), \(k_2\) and \(k_3 = k_1\) represent the three values of exact (spectral) absorption coefficient respectively as shown in Fig. 3. Comparing the results of (6) and (7), it is possible to determine which frequency will represent the global minimum.

Unfortunately this easy determination of the global minimum is only possible in the case of an isothermal plasma. In the case of a non-isothermal plasma, it is not easy to determine which break point frequency \(p_\nu \) is going to be associated with the global minimum. This is demonstrated in Fig. 3b where the global minimum is located differently for profile 1, even though all the temperature profiles span the same temperature range.

Note that the steepness of the norm \({\varDelta} {F_{\nu}}\) around the minimum is much lower compared to the previous test. Also the relative decrease of the norm \({\varDelta} {F_{\nu}}\) at the location of the minimum is much smaller compared to the previous test, especially at higher temperatures. The implication is that using the two-band approximation leads to significant errors even in case of relatively simple test cases. Using exact (spectral) absorption coefficients with a relatively small step-like change (only one order of magnitude) also contributes to this effect. Using exact absorption coefficients with much larger variance would yield to better relative reduction of norm \({\varDelta} {F_{\nu}}\), but the absolute value of norm \({\varDelta} {F_{\nu}}\) would be very high indicating large errors. This is partially demonstrated in the next test case.

Test 3

In the previous test we defined a trench like profile of the exact (spectral) absorption coefficient and investigated the dependency of norm \({\varDelta} {F_{\nu}}\) on the plasma temperature profile. In this third test we determine the influence of the depth of the trench like exact (spectral) absorption profile on the norm and the position of the norm’s global minimum. We gradually decrease the depth of the trench profile by increasing the minimum values of the absorption coefficient inside the trench, eventually changing the trench like profile into a hill like profile. In the previous test it was also shown that it is possible to exactly determine the minima position for the case of an isothermal plasma. Similar behavior was observed for different trench depths and isothermal plasma temperatures. Therefore we skip the calculation for the isothermal plasma approximation in this test and apply only one temperature profile, which is profile 2 as shown in Fig. 1.

Due to the variation of the trench depth, the norm \({\varDelta} {F_{\nu}}\) is varying too as shown in Fig. 4. With smaller depth of the trench like profile, the minimum at the position of the step-like change in the exact (spectral) absorption coefficient gradually evolves becoming the position of the maximum of \({\varDelta} {F_{\nu}}\) and it is even possible to turn it into the global maximum. The position of global minimum is then shifted to an undetermined frequency inside the trench.

This result is very important as it demonstrates that under certain circumstances like small changes in the spectral absorption coefficient or varying temperature profile, the selection of the break point location at the position of the step-like change in the spectral absorption coefficient would be the worst possible option.

The general behaviour of the norm \({\varDelta} {F_{\nu}}\) does not change when the trench like exact absorption profile is changed to a hill like profile. The position of the minimum slowly reverts back to position of the step-like change as the height of the hill increases.

Unlike the former test cases, the value of reduced norm now depends on the depth or height of the trench or hill respectively. All of the reduced norm are located between values \(3\times 10^{-5}\) and 0.007 with each individual reduced norm profile having a span of approximately 0.001.

Fig. 4
figure 4

The difference between exact and two band model as the function of the break point location (frequency integration boundary) for the temperature profile 2. The case a represents different trench depth and b different hill height. This figure illustrates results from test 3

Full size image

Test 4

The previous test proved that placing the breaking point \(p_\nu \) at the frequency of the jump in exact absorption coefficient might not be the best option. It is true only in case of isothermal plasma assumption. The position of the minimum of \({\varDelta} {F_{\nu}}\) can be shifted to some undetermined frequency. The question now is whether the frequency of the minimum is determined by the temperature profile itself or just the temperature range. This fourth test case is designed to answer that question.

For the purpose of this test we defined an exact (spectral) absorption coefficient profile with a relatively shallow trench. In the previous test is was shown that for one specific temperature profile this is enough to move the global minimum of the norm \({\varDelta} {F_{\nu}}\) away from the step-like change in the exact absorption coefficient. Figure 5a shows that the minimum displacement is valid for every considered temperature profile. It also demonstrates that the position of the global minimum depends on the temperature profile and cannot be easily determined from the exact absorption coefficient alone.

The results of this test might look unimportant, especially because the reduced norm for this test corresponding to Fig. 5a varies between \(3\times 10^{-4}\) and \(7\times 10^{-4}\) only. We achieved this result using a very small range of absorption coefficient, whereas the real absorption coefficient can easily vary between \(10^{-3}\) and \(10^{6}\) m\(^{-1}\). To evaluate the behaviour of the norm \({\varDelta} {F_{\nu}}\) and to emphasize the importance of this result we investigated an additional absorption coefficient profile. The new exact (spectral) absorption coefficient has the same trench-like profile but varies between the values \(10^{-2}\) inside the trench and \(10^3\) everywhere else. The corresponding values of the norm \({\varDelta} {F_{\nu}}\), shown in Fig. 5b, are completely different from the previous results in Fig. 5a and even from Fig. 3b. The temperature profiles have much larger impact now, as two of the profiles locate the minimum to the position of the second step-like change while the third temperature profile locates the minimum in the middle of the trench. The impact of this new exact absorption coefficient is also larger. The reduced norm values corresponding to Fig. 5b vary between 0.4 and 0.3 for temperature profile 1 and between 0.9 and 0.6 for temperature profiles 2 and 3.

Note that the results in Fig. 5b might be somewhat distorted by the fact that in majority of the frequency range the medium can be considered optically thick. As mentioned before the unmodified Planck averaging (1) does not handle optically thick medium very well. For the sake of continuity we decided to keep the unmodified Planck averaging even though a better results could probably be achieved using modified Planck averaging.

Fig. 5
figure 5

The difference between exact and two band model as the function of the break point location (frequency integration boundary) for different temperature profiles. Small difference in absorption coefficient (a) and large difference (b) are shown. Note that figures do not use a logarithmic scale. This figure illustrates results from test 4

Full size image

Test 5

In all previous test cases we were using exact (spectral) absorption coefficient profiles with a step function. This closely represents the MAC approximation, however it is not the most accurate approximation of the continuum radiation which is usually used for the selection of MAC band boundaries [14]. The more accurate description was provided by Liebermann and Lowke [15], suggesting the absorption decays with a factor of \(1/\nu ^3\) from some absorption edge value.

To represent the spectral absorption coefficient of a thermal plasma more realistic, we are defining the exact (spectral) absorption coefficient in a similar way. The exact absorption coefficient is decreasing with \(1/\nu ^3\) with two step-like changes positioned at the same frequencies as in the previous test cases. We also added a small constant value to the exact absorption coefficient so it does not asymptotically approach zero at higher frequencies. The final exact absorption coefficient is depicted in Fig. 6.

We calculated the norm \({\varDelta} {F_{\nu}}\) the same way as in the previous test cases. The previous results indicated that in case of a constant temperature profile, the minimum of the norm is located at the position of the sharp change in the exact absorption coefficient. This holds true also for the profile varying with \(1/\nu ^3\) and case of relatively large edge change as shown in Fig. 6a. However the relative height of the edge also plays an important role. The second, relatively smaller edge in the exact absorption coefficient does produce a local maximum of the norm \({\varDelta} {F_{\nu}}\) rather than a local minimum.

In case of a varying temperature profile, the global minimum of the norm is shifted as is shown in Fig. 6b. The same behaviour was observed in the previous test cases. The position of the minimum is related to the temperature profile itself, thus cannot be determined by the variation of the exact absorption coefficient only. This is the exact same conclusion that was drawn from the previous test cases.

The relative error expressed by the reduced norm is comparable with the other test cases. Its value varies between 0.003 at the maximum and 0.001 at the minimum for the majority of the temperature profiles. The notable exception is the 10 kK constant temperature profile with the maximum value of approximately 0.004.

Fig. 6
figure 6

The difference between exact and two band model as the function of the break point location (frequency integration boundary) for constant (a) and varying (b) temperature profiles. This figure illustrates results from test 5. Note that b does not use a logarithmic scale

Full size image

More Realistic Spectrum

In the previous section we considered deliberately defined exact absorption coefficients to prove that the break point selection has an important effect on the overall model accuracy. However those profiles did not match any absorption coefficient that would exist in a real thermal plasma. In this section we apply the same evaluation process applying more realistic absorption coefficients.

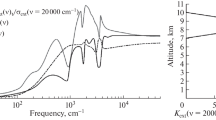
In order to calculate the absorption coefficient of a thermal plasma, the temperature and therefore the composition has to be known. First we calculated the plasma composition of air at 20 kK and 1 bar, according to [16] with species standard thermodynamic functions taken over from [17]. The spectral absorption coefficient was then calculated with the approach given by Aubrecht et al. [18] and is shown in Fig. 7.

The evaluated norm \({\varDelta} {F_{\nu}}\) is also shown in Fig. 7. It clearly demonstrates that using the only continuum variation in order to define the integration boundaries would not produce the best result in terms of accuracy. A better positioning of the break points should consider the position of the resonance lines. This is mainly caused by the application of the Planck mean averaging approach to calculate the MAC, which is known to overestimate the importance of lines [6].

The second important result is that the norm \({\varDelta} {F_{\nu}}\) is a discontinuous function of the frequency, as demonstrated in Fig. 7. One can see that even small variations in the selection of the integration boundaries can lead to large variation in the accuracy of the MAC based radiation model. Due to this fact as well as the complexity of the absorption spectrum of a thermal plasma, the selection of the integration boundaries for MAC calculation should be done by means of an numerical optimization algorithm, which is capable of finding the global minimum of the norm \({\varDelta} {F_{\nu}}\). The applied optimization procedure has to deal with several local minima and a non-continuous target function.

It is worth noting that even though in the previous section the values of the reduced norm were quite small, those values are two orders of magnitude higher when the realistic spectrum is considered . It is partially caused by the utilization of Planck averaging without line treatment. But even with the line treatment the relative improvement based on break point location would be much higher than in previous section.

Fig. 7
figure 7

The difference between exact and two-band model as function of the break point location (frequency integration boundary) for air at a temperature of 20 kK and a pressure of 1 bar. Note that this figure is plotted using the reduced norm

Full size image

Conclusion

In this paper we demonstrated the difficulties in the process of band selection for the calculation of Planck averaged mean absorption coefficients for thermal plasma radiation modeling. By means of several test cases we showed, that the selection of frequencies in the spectrum where the absorption coefficient jumps as integration boundaries can introduce a significant error in the radiation transport model. The optimal integration boundary (break point) can be a non-specific frequency in the spectrum where the absorption coefficient is more or less constant.

In addition we used our established procedure to evaluate the accuracy of the two-band model, using Planck averaged absorption coefficient based on the calculated spectrum of an air plasma at 20 kK and 1 bar. It was shown that using the continuum contribution of the spectrum only to determine the integration interval for the Planck averaging can be misleading. The interval providing more accurate radiation model results is at the frequency of the resonance lines, rather than at the jump in the continuum contribution of the absorption spectrum.

In summary the results lead to the conclusion that the band selection process for the radiation modeling in thermal plasmas cannot be done successfully without the aid of a numerical optimization procedure. The norm \({\varDelta} {F_{\nu}}\) defined in (2) is the obvious choice for the objective function. It is quite flexible with the ability to emphasize certain spacial areas by the usage of weighting factors. The procedure has to be able to handle several local minima and the discontinuous behaviour of the target function. Without this optimization procedure the band selection process can introduce unnecessary and unexpected errors into the radiation transfer evaluation while using MAC. With the deployment of the optimization procedure it is much more likely that for a certain wide range of parameters (temperature range, plasma composition, pressure, MAC calculation method) it would be possible to find an universal set of band boundaries.